Temas Del Año

• Area Y Perímetros De Figuras Solidas

• Concepto De Linea-Punto-Segmento

Área Y Perímetros De Figuras Solidas

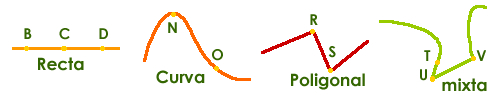
ÁREA Y PERÍMETROS:

PERÍMETRO Y ÁREA DEL CUADRADO

PERÍMETRO  

El perímetro de un cuadrado es cuatro veces el valor del lado

    P = 4 ·a

ÁREA  

El área de un cuadrado es igual al cuadrado de la longitud del lado.  

A= a²

1. PERÍMETRO Y ÁREA DEL RECTÁNGULO

                                                 

                                                 PERÍMETRO

El rectángulo tiene los lados iguales dos a dos, por tanto:

P = 2· a + 2· b

ÁREA

El área de un rectángulo es el producto de la longitud de los lados.

A= a · b

                          PARALELOGRAMO

El paralelogramo de la derecha tiene el mismo área que el rectángulo que tiene debajo. Mueve el punto que se indica.

Por tanto el área del paralelogramo es el mismo que el del rectángulo.

A = b · a

Siendo b  un lado y a  la altura.

PERÍMETRO Y ÁREA DE UN PARALELOGRAMO.

PERÍMETRO                                                                      P = 2· b + 2· c =                                                                    = 2 (b + c)

ÁREA

El área de un paralelogramo es igual al producto de la base por la altura.

A=   b · a

ROMBO

El rombo es un paralelogramo (que tiene los cuatro lados iguales) por tanto su perímetro y área pueden calcularse como los de un paralelogramo. La expresión más habitual es en función del valor de sus diagonales, que como sabes, son perpendiculares en un rombo. El rombo de la figura (amarillo) tiene área la mitad del rectángulo. Mueve los vértices para comprobar que siempre es así. Los lados del rectángulo son las diagonales del rombo. Por tanto el área del rombo es : D y d son los valores de las diagonales. PERÍMETRO Y ÁREA DE UN ROMBO ÁREA El área del rombo es igual al producto de diagonales dividido entre dos. PERÍMETRO El perímetro del rombo es cuatro veces el valor del lado. P = 4· L El valor de las diagonales y el lado, están relacionados.

El valor de las diagonales y el lado, están relacionados.

El triángulo de color es rectángulo, aplicando el teorema de Pitágoras:

Como sabes el cuadrado es un caso particular de rombo.

Es un rombo que tiene las diagonales iguales.

Para calcular el área del cuadrado puedes utilizar también la expresión del área del rombo.

Comprueba en la figura que estas expresiones dan el mismo valor.

TRAPECIO

Recuerda que el trapecio es un cuadrilátero con dos lados paralelos, que se llaman bases y otros dos no paralelos. La figura de la derecha representa un trapecio. Mueve el botón rojo. El trapecio que aparece tiene igual área y entre los dos son un paralelogramo de base B + b y de altura a. Por tanto el área del trapecio es: ÁREA Y PERÍMETRO DE UN TRAPECIO ÁREA El área del trapecio es igual a la semisuma de las bases por la altura. PERÍMETRO Para calcular el perímetro de un trapecio cualquiera se suma el valor de los cuatro lados. TRAPECIO ISÓSCELES Y TRAPECIO RECTÁNGULO Tanto en el trapecio isósceles como en el rectángulo podemos aplicar el Teorema de Pitágoras a los triángulos rectángulos que se representan. Se obtiene una relación entre B, b, L y a. Podemos calcular uno cualquiera de estos valores conociendo los restantes.                            TRIÁNGULO Podemos deducir la expresión del área de un triángulo a partir del área de un paralelogramo. El área del triángulo ABC es la mitad de la del paralelogramo ABCD (Mueve el botón ) de base b y altura a. Por tanto el área del triángulo es ÁREA Y PERÍMETRO DE UN TRIÁNGULO PERÍMETRO Suma de sus lados P= b + c + d ÁREA El área de un triángulo es el producto de uno de sus lados por la altura sobre él dividido entre dos.                                                                          POLÍGONOS REGULARES Un polígono regular de N lados se puede dividir en N  triángulos isósceles. El área del polígono regular es por tanto : A Polígono Regular = N · A Triángulo , esto es El Perímetro  es la longitud de un lado por el número de lados. P = N · L  Click aquí para ver explicación completa                                       FIGURAS SOLIDAS Se denominan figuras sólidas ó cuerpos geométricos a aquellos elementos que, ya sean reales o ideales. — que existen en la realidad o pueden concebirse mentalmente. — ocupan un volumen en el espacio desarrollándose por lo tanto en las tres dimensiones de alto, ancho y largo; y están compuestos por figuras geométricas. Entre los cuerpos geométricos estan: El cubo — que está compuesto por seis caras cuadradas; motivo por el cual se le conoce también con el nombre de exaedro regular, (exaedro = cuerpo con 6 caras). El tetraedro regular — compuesto por cuatro caras con forma de triángulos equiláteros. El octaedro regular — compuesto por ocho caras con forma de triángulos equiláteros, en forma de dos pirámides unidas por sus base. El icosaedro regular — compuesto por veinte caras con forma de triángulos equiláteros, que tiene un eje plano exagonal. El dodecaedro regular — compuesto por doce caras con forma de pentágono. El prisma — que está compuesto por caras laterales rectangulares (que pueden ser cuadradas); y bases con forma de triángulo, cuadrado (salvo cuando las caras también lo son, en cuyo caso es un cubo), pentágono, exágono u otro polígono regular. El prisma oblicuo — que es similar al prima, pero con dos lados de forma romboidal; por lo cual solamente puede tener bases cuadradas. La pirámide recta — compuesto por una base con forma de polígono regular, y lados triangulares cuya base son los lados del polígono, y unen todos su vértices en un mismo punto, también llamado vértice de la pirámide; el cual se encuentra sobre la perpendicular a la base que pasa por su centro. La pirámide inclinada — similar a la anterior, pero cuyo vértice se encuentra sobre una perpendicular a la base que no pasa por su centro. El cilindro — que está compuesto dos bases circulares y una superficie curva continua, equivalente a un rectángulo. El cono — compuesto por una base circular, y una superficie curva que la rodea y se une en un vértice que se encuentra sobre la perpendicular a la base que pasa por su centro. El cono truncado — que siendo similar a un cono, tiene una base conformada por un plano inclinado, con lo cual adopta una forma de elipse. La esfera — que es circular en todos sus planos centrales. La semiesfera — que es una esfera que ha sido cortada por uno de sus planos circulares, de manera que tiene una base circular y una cúpula esférica. Click aquí para ver explicación completa TALLER: 1.- Calcula el perimetro y el area de un cuadro de lado  4 m 2.- La base de un rectangulo es 5 m.Y la altura la mitad de la base.Calcula el area y el perimetro. 3.- El área de un cuadrado es 5,76 cm2 . Calcula el perímetro del cuadrado. 4.-La base de un paralelogramo es 5 cm, y su altura es 2,8 cm. ¿Cual es el área del paralelogramo? Con los datos anteriores (base y altura), ¿se puede calcular el perímetro? Toma las medidas que necesites utilizando el segmento auxiliar para determinar el perímetro. 5.- La diagonal mayor de un rombo mide 5m, y la menor es la mitad. Calcula el área y el perímetro del rombo. Debes de utilizar el teorema de Pitágoras. 6.- Calcula el área de un cuadrado de 4 m. de diagonal. a) Utilizando el teorema de Pitágoras para determinar el lado.        b) Utilizando la expresión A = D · d / 2 Click aquí para hacer autoevaluación         Ver taller

Concepto De Linea Punto Y Segmento

LINEA

La línea geométrica por definición es un arte invisible. Es la traza que el punto deja al moverse y por lo tanto es un producto suyo. Surge de la alteración del reposo total del punto. Con ella se salta de una situación estática a una dinámica. La línea se halla en el extremo opuesto al elemento primario, es decir al punto, y constituye un elemento derivado o secundario.
Click aquí para ver explicación completa

Ejemplos:


Ver mas ejemplos

PUNTO:

En geometría, el punto es uno de los entes fundamentales, junto con la recta y el plano. Son considerados conceptos primarios, es decir, que sólo es posible describirlos en relación con otros elementos similares. Se suelen describir apoyándose en los postulados característicos, que determinan las relaciones entre los entes geométricos fundamentales.

El punto es una «figura geométrica» adimensional: no tiene longitud, área, volumen, ni otro ángulo dimensional. No es un objeto físico. Describe una posición en el espacio, determinada respecto de un sistema de coordenadas preestablecido.

Conceptos básicos

Para el estudio de la geometría, es indispensable conocer el concepto intuitivo de punto, recta y plano. Estos son términos no definidos que proveen el inicio de la geometría.
Punto es el objeto fundamental en geometría, el punto representa solo posición y no tiene dimensión, es decir, largo cero, ancho cero y altura cero. Se representan por letras mayúsculas.

Click aquí para ver explicación completa

Ejemplo:

Tres puntos
Ver mas ejemplos SEGMENTO
Un segmento, en geometría, es un fragmento de recta que está comprendido entre dos puntos.
Así, dados dos puntos A y B, se le llama segmento AB a la intersección de la semirrecta de origen A que contiene al punto B, y la semirrecta de origen B que contiene al punto A. Luego, los puntos A y B se denominan extremos del segmento, y los puntos de la recta a la que pertenece el segmento (recta sostén), serán interiores o exteriores al segmento según pertenezcan o no a este. Click aquí para ver explicación completa Ejemplo:
TALLER Click aquí para ver taller